重温数据结构-排序篇
重温数据结构-排序篇
数据结构中的排序算法是最基础的算法知识,但是长时间不碰,导致很多实现细节不太清楚,所以决定重新手写一下经典排序算法。
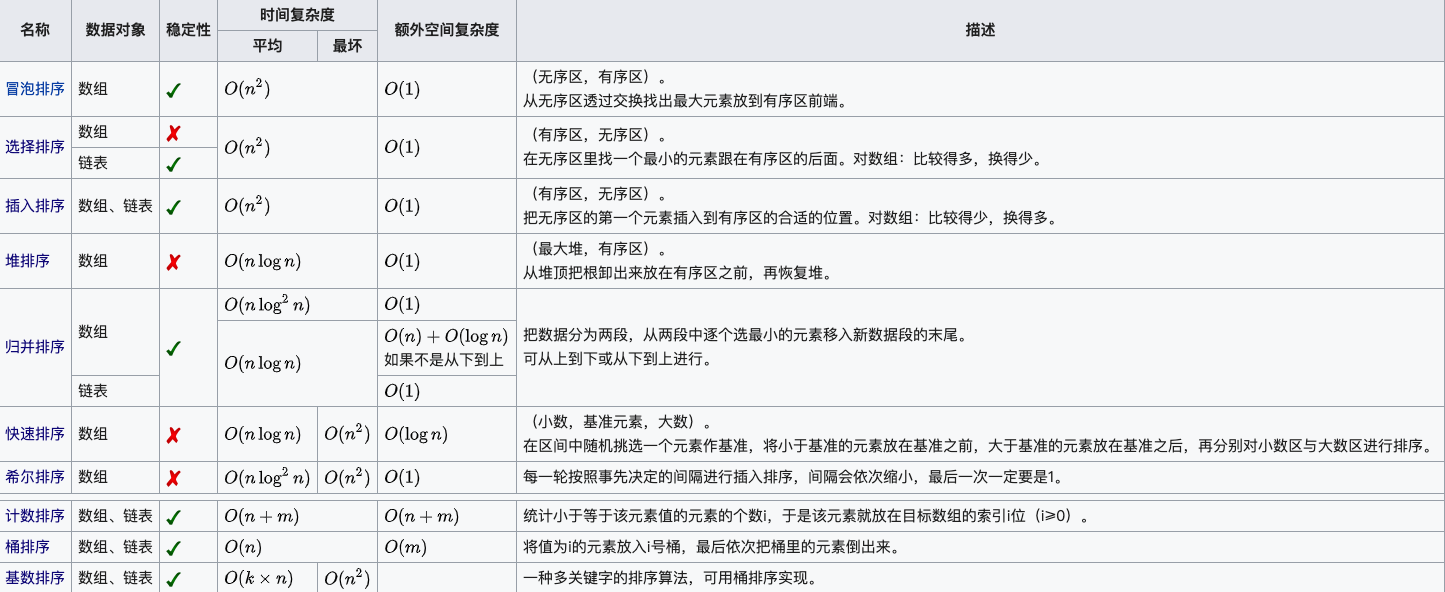
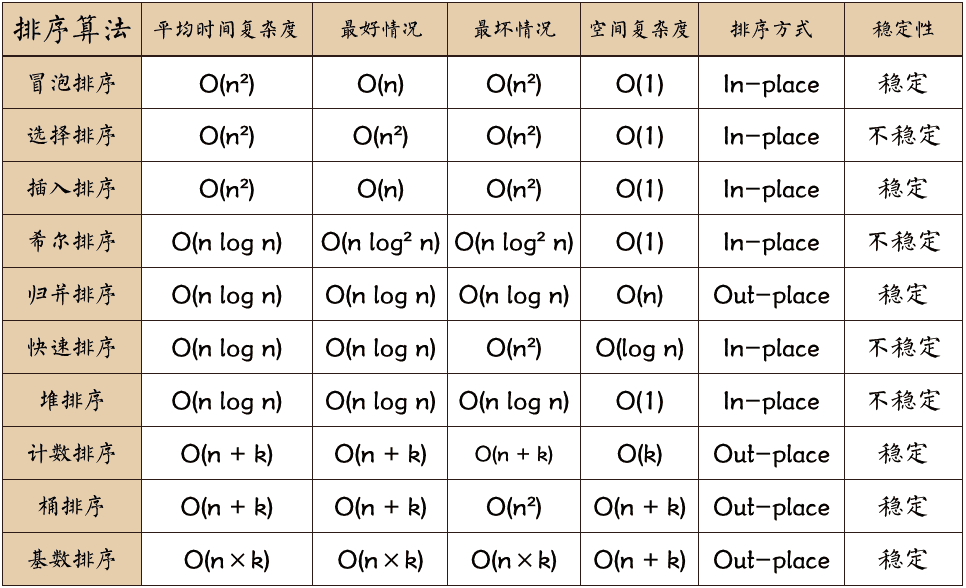
TIP额外空间复杂度为O(1)就是原地排序
1. 冒泡排序
从无序区通过两两比较,将最大(最小)的元素交换到无序区的末尾,逐步缩小无序区,直到无序区为空。
动画演示未加标记版
C++ 实现
冒泡排序cpp实现
void bubbleSort(int arr[], int n){
for(int i = 0;i < n-1;i++){
bool flag = false;
for(int j = 0;j < n-1-i;j++){
if(arr[j] > arr[j+1]){ //稳定
int tmp = arr[j];
arr[j] = arr[j+1];
arr[j+1] = tmp;
flag = true;
}
}
if(!flag) break; // 提前结束优化
}
}IMPORTANT稳定
额外空间复杂度:
时间复杂度: ,带flag下的最好复杂度为
2. 选择排序
从无序区选择最大(最小)的元素,放到无序区的末尾,逐步缩小无序区,直到无序区为空。
动画演示
C++ 实现
选择排序cpp实现
void selectionSort(int arr[], int n){
for(int i = 0;i < n-1;i++){
int minIndex = i;
for(int j = i+1;j < n;j++){// j = i也不保证稳定,如[4a, 4b, 2]
if(arr[j] < arr[minIndex]){
minIndex = j;
}
}
if(minIndex != i){
int tmp = arr[i];
arr[i] = arr[minIndex];
arr[minIndex] = tmp;
}
}
}IMPORTANT不稳定
额外空间复杂度:
时间复杂度:
3. 插入排序
从无序区选择一个元素,插入到有序区中,逐步缩小无序区,直到无序区为空。
动画演示
C++ 实现
插入排序cpp实现
void insertionSort(int arr[], int n){
for(int i = 1;i < n;i++){
int key = arr[i];
int j = i - 1;//i 到 j-1 为有序区
while(j >= 0 && arr[j] > key){ //稳定
arr[j + 1] = arr[j];
j--;
}
arr[j + 1] = key;
}
}IMPORTANT稳定
额外空间复杂度:
时间复杂度:,最好复杂度为
4. 希尔排序
希尔排序是插入排序的改进,通过间隔来缩小无序区,从而提高效率。
动画演示
C++ 实现
希尔排序实现
void shellSort(int arr[], int n){
for(int gap = n / 2; gap > 0; gap /= 2){
for(int i = gap; i < n; ++i){
int temp = arr[i];
int j = i;
// 对间隔为 gap 的子序列进行插入排序
while(j >= gap && arr[j - gap] > temp){
arr[j] = arr[j - gap];
j -= gap;
}
arr[j] = temp;
}
}
}IMPORTANT不稳定
额外空间复杂度:
平均时间复杂度:, 最坏复杂度为,使用Knuth 序列最好复杂度为
希尔排序趟数结果
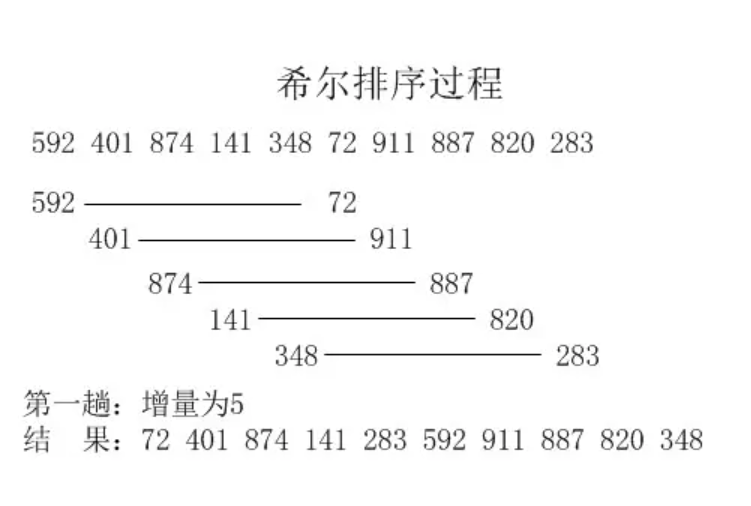

:::
5. 快速排序
快速排序通过分治法,将数组分为两个子数组,左边的元素都小于等于中间元素,右边的元素都大于等于中间元素,然后递归对左右子数组进行排序。
动画演示
C++ 实现
快速排序cpp实现
int Paritition1(int A[], int low, int high) {
int pivot = A[low];//选择第一个作为基准元素
while (low < high) {
while (low < high && A[high] >= pivot) {
--high;
}
A[low] = A[high];
while (low < high && A[low] <= pivot) {
++low;
}
A[high] = A[low];
}
A[low] = pivot;
return low;
}
void QuickSort(int A[], int low, int high) //快排母函数
{
if (low < high) {
int pivot = Paritition1(A, low, high);//划分
QuickSort(A, low, pivot - 1);
QuickSort(A, pivot + 1, high);
}
}IMPORTANT不稳定
额外空间复杂度:
时间复杂度:, 最坏复杂度为,最好复杂度为
6. 归并排序
归并排序是分治法,将数组分为两个子数组,然后对子数组进行排序,最后合并两个有序数组。
动画演示
C++ 实现
归并排序cpp实现
void Merge(int a[], int left, int mid, int right){
int temp[right - left + 1]; //临时数组用于存储排序时的数
int i = left; //分成两块 i指向左边的数字 j指向右边的数字
int j = mid + 1;
int k = 0; //k用于存储数字到临时数组
while( i <= mid && j <= right ){
if(a[i] < a[j]) //永远都是 i 和 j 指向的数进行比较
temp[k++] = a[i++]; //谁小,谁就先放到临时数组中
else
temp[k++] = a[j++];
}
while( i <= mid ) //如果左边还有数没放上去,就依次放上去
temp[k++] = a[i++];
while( j <= right ) //如果是右边还有同上
temp[k++] = a[j++];
for(int m = left, n = 0; m <= right; m++, n++)//读取临时数组中的数
a[m] = temp[n];
}
void Merge_Sort(int a[], int left, int right){
if( left == right )
return;
int mid = (left + right)/2;
void Merge(int a[], int left, int mid, int right){
int temp[right - left + 1]; //临时数组用于存储排序时的数
int i = left; //分成两块 i指向左边的数字 j指向右边的数字
int j = mid + 1;
int k = 0; //k用于存储数字到临时数组
while( i <= mid && j <= right ){
if(a[i] < a[j]) //永远都是 i 和 j 指向的数进行比较
temp[k++] = a[i++]; //谁小,谁就先放到临时数组中
else
temp[k++] = a[j++];
}
while( i <= mid ) //如果左边还有数没放上去,就依次放上去
temp[k++] = a[i++];
while( j <= right ) //如果是右边还有同上
temp[k++] = a[j++];
for(int m = left, n = 0; m <= right; m++, n++)//读取临时数组中的数
a[m] = temp[n];
}
void Merge_Sort(int a[], int left, int right){
if( left == right )
return;
int mid = (left + right)/2;
//递归拆分成较小规模子序列排序
Merge_Sort(a, left, mid);
Merge_Sort(a, mid + 1, right);
Merge(a, left, mid, right); //合并较小规模问题解
}IMPORTANT稳定
额外空间复杂度:
时间复杂度:, 最坏复杂度为,最好复杂度为
7. 堆排序
堆排序是分治法,将数组构建成堆(),然后依次取出堆顶元素,将剩余元素重新构建成堆,直到堆为空。
动画演示

C++ 实现
堆排序cpp实现
// 堆调整函数:维护以i为根的子树为最大堆
void heapify(vector<int>& arr, int n, int i) {
int largest = i; // 初始化最大元素为根节点
int left = 2 * i + 1; // 左子节点索引
int right = 2 * i + 2; // 右子节点索引
// 如果左子节点大于根节点
if (left < n && arr[left] > arr[largest]) {
largest = left;
}
// 如果右子节点大于当前最大元素
if (right < n && arr[right] > arr[largest]) {
largest = right;
}
// 如果最大元素不是根节点
if (largest != i) {
swap(arr[i], arr[largest]);
// 递归调整受影响的子树
heapify(arr, n, largest);
}
}
// 堆排序主函数
void heapSort(vector<int>& arr) {
int n = arr.size();
// 构建最大堆(从最后一个非叶子节点开始调整)
// 堆调整函数:维护以i为根的子树为最大堆
void heapify(vector<int>& arr, int n, int i) {
int largest = i; // 初始化最大元素为根节点
int left = 2 * i + 1; // 左子节点索引
int right = 2 * i + 2; // 右子节点索引
// 如果左子节点大于根节点
if (left < n && arr[left] > arr[largest]) {
largest = left;
}
// 如果右子节点大于当前最大元素
if (right < n && arr[right] > arr[largest]) {
largest = right;
}
// 如果最大元素不是根节点
if (largest != i) {
swap(arr[i], arr[largest]);
// 递归调整受影响的子树
heapify(arr, n, largest);
}
}
// 堆排序主函数
void heapSort(vector<int>& arr) {
int n = arr.size();
// 构建最大堆(从最后一个非叶子节点开始调整)
for (int i = n / 2 - 1; i >= 0; i--) {
heapify(arr, n, i);
}
// 逐个提取堆顶元素(最大元素)
for (int i = n - 1; i > 0; i--) {
// 将堆顶元素交换到数组末尾
swap(arr[0], arr[i]);
// 对剩余元素重新调整为最大堆
heapify(arr, i, 0);
}
}
```cppIMPORTANT不稳定
额外空间复杂度:
时间复杂度:, 最坏复杂度为,最好复杂度为
8. 计数排序
适用于整数或对有限范围内的元素排序,通过统计每个元素出现的次数,然后根据计数结果构建排序后的数组。
动画演示

C++ 实现
计数排序cpp实现
vector<int> countingSort(vector<int> arr, int maxValue) {
int bucketLen = maxValue + 1;
vector<int> bucket(bucketLen, 0); // 初始化计数桶
int sortedIndex = 0;
int arrLen = arr.size();
// 统计每个元素出现次数
for (int i = 0; i < arrLen; ++i) {
bucket[arr[i]]++;
}
// 根据计数桶重构排序后的数组
for (int j = 0; j < bucketLen; ++j) {
while (bucket[j] > 0) {
arr[sortedIndex] = j;
sortedIndex++;
bucket[j]--;
}
}
return arr;
}IMPORTANT稳定
额外空间复杂度: 是数值范围
时间复杂度最好最坏都是:
9. 桶排序
适用于数字范围较小的情况,将数字分配到相应的桶中,然后对每个桶进行排序,最后将排序后的桶按顺序合并成排序后的数组。
动画演示
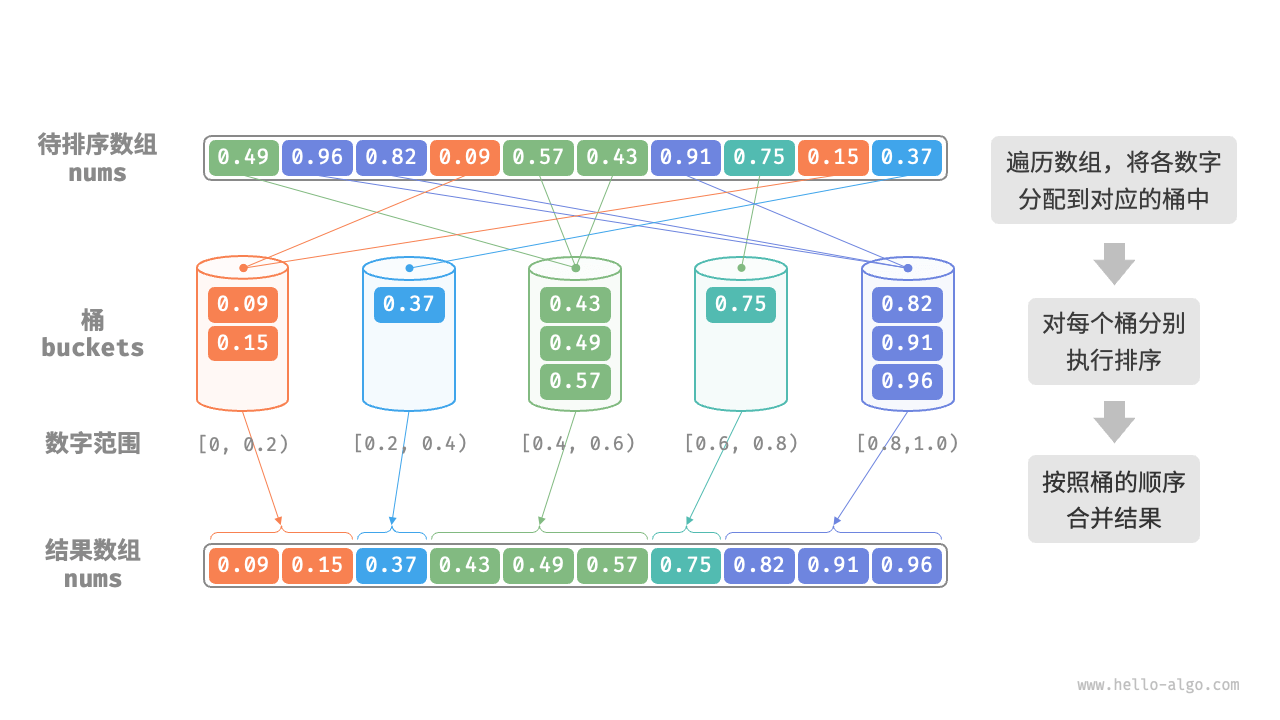
C++ 实现
桶排序cpp实现
void bucketSort(vector<float> &nums) {
// 初始化 k = n/2 个桶,预期向每个桶分配 2 个元素
int k = nums.size() / 2;
vector<vector<float>> buckets(k);
// 1. 将数组元素分配到各个桶中
for (float num : nums) {
// 输入数据范围为 [0, 1),使用 num * k 映射到索引范围 [0, k-1]
int i = num * k;
// 将 num 添加进桶 bucket_idx
buckets[i].push_back(num);
}
// 2. 对各个桶执行排序
for (vector<float> &bucket : buckets) {
// 使用内置排序函数,也可以替换成其他排序算法
sort(bucket.begin(), bucket.end());
}
// 3. 遍历桶合并结果
int i = 0;
for (vector<float> &bucket : buckets) {
for (float num : bucket) {
nums[i++] = num;
}
}
}IMPORTANT稳定
额外空间复杂度:
时间复杂度:, 最坏复杂度为,最好复杂度为
10. 基数排序
适用于整数或对有限范围内的元素排序,通过将数字按位分类,然后按顺序合并成排序后的数组。
动画演示

C++ 实现
基数排序cpp实现
/* 获取元素 num 的第 k 位,其中 exp = 10^(k-1) */
int digit(int num, int exp) {
// 传入 exp 而非 k 可以避免在此重复执行昂贵的次方计算
return (num / exp) % 10;
}
/* 计数排序(根据 nums 第 k 位排序) */
void countingSortDigit(vector<int> &nums, int exp) {
// 十进制的位范围为 0~9 ,因此需要长度为 10 的桶数组
vector<int> counter(10, 0);
int n = nums.size();
// 统计 0~9 各数字的出现次数
for (int i = 0; i < n; i++) {
int d = digit(nums[i], exp); // 获取 nums[i] 第 k 位,记为 d
counter[d]++; // 统计数字 d 的出现次数
}
// 求前缀和,将“出现个数”转换为“数组索引”
for (int i = 1; i < 10; i++) {
counter[i] += counter[i - 1];
}
// 倒序遍历,根据桶内统计结果,将各元素填入 res
vector<int> res(n, 0);
for (int i = n - 1; i >= 0; i--) {
int d = digit(nums[i], exp);
int j = counter[d] - 1; // 获取 d 在数组中的索引 j
/* 获取元素 num 的第 k 位,其中 exp = 10^(k-1) */
int digit(int num, int exp) {
// 传入 exp 而非 k 可以避免在此重复执行昂贵的次方计算
return (num / exp) % 10;
}
/* 计数排序(根据 nums 第 k 位排序) */
void countingSortDigit(vector<int> &nums, int exp) {
// 十进制的位范围为 0~9 ,因此需要长度为 10 的桶数组
vector<int> counter(10, 0);
int n = nums.size();
// 统计 0~9 各数字的出现次数
for (int i = 0; i < n; i++) {
int d = digit(nums[i], exp); // 获取 nums[i] 第 k 位,记为 d
counter[d]++; // 统计数字 d 的出现次数
}
// 求前缀和,将“出现个数”转换为“数组索引”
for (int i = 1; i < 10; i++) {
counter[i] += counter[i - 1];
}
// 倒序遍历,根据桶内统计结果,将各元素填入 res
vector<int> res(n, 0);
for (int i = n - 1; i >= 0; i--) {
int d = digit(nums[i], exp);
int j = counter[d] - 1; // 获取 d 在数组中的索引 j
res[j] = nums[i]; // 将当前元素填入索引 j
counter[d]--; // 将 d 的数量减 1
}
// 使用结果覆盖原数组 nums
for (int i = 0; i < n; i++)
nums[i] = res[i];
}
/* 基数排序 */
void radixSort(vector<int> &nums) {
// 获取数组的最大元素,用于判断最大位数
int m = *max_element(nums.begin(), nums.end());
// 按照从低位到高位的顺序遍历
for (int exp = 1; exp <= m; exp *= 10)
// 对数组元素的第 k 位执行计数排序
// k = 1 -> exp = 1
// k = 2 -> exp = 10
// 即 exp = 10^(k-1)
countingSortDigit(nums, exp);
}IMPORTANT稳定
设数据量为 、数据为 进制、最大位数为
额外空间复杂度:
时间复杂度: