树

二叉树

二叉树可以结点为0，但是树的结点最少为1
完全二叉树：倒数第二层是满的，且最后一层必须左对齐

二叉树性质

性质 1： 一棵非空二叉树的第 $i$ 层上至多有 $2^{i - 1}$ 个结点（$i \geq 1$）。

性质 2： 深度为 $h$ 的二叉树至多有 $2^h - 1$ 个结点（其中 $h \geq 1$）。

性质 3： 对于任何一棵二叉树 $T$，如果其终端结点数（叶子结点数）为 $n_0$，度为 2 的结点数为 $n_2$，则 $n_0 = n_2 + 1$。

性质 4： 具有 $n$ 个结点的完全二叉树的深度为 $\lfloor \log_2 n \rfloor + 1$（其中 $\lfloor x \rfloor$ 表示不大于 $x$ 的最大整数）。

性质 5： 对于具有 $n$ 个结点的完全二叉树，如果按照从上到下、同一层次上的结点按从左到右的顺序对二叉树中的所有结点从 1 开始顺序编号，则对于序号为 $i$ 的结点，有：

1. 双亲结点： 如果 $i > 1$，则序号为 $i$ 的结点的双亲结点的序号为 $\lfloor i/2 \rfloor$（$\lfloor i/2 \rfloor$ 表示对 $i/2$ 的值取整）。如果 $i = 1$，则结点 $i$ 为根结点，没有双亲。
2. 左孩子结点： 如果 $2i > n$，则结点 $i$ 无左孩子（此时结点 $i$ 为终端结点）；否则其左孩子结点的序号为 $2i$。
3. 右孩子结点： 如果 $2i + 1 > n$，则结点 $i$ 无右孩子；否则其右孩子结点的序号为 $2i + 1$。

树的遍历

前序遍历、后序遍历、层序遍历

二叉树的遍历

前中后三种遍历，两种遍历方式(一定要包含中序遍历)才能确定唯一二叉树

森林的遍历

前序遍历和后序遍历
① 前序遍历森林 ≡ 前序遍历该森林转换为的二叉树；
② 后序遍历森林 ≡ 中序遍历该森林转换为的二叉树；
③ 前序遍历树 ≡ 前序遍历该树对应的二叉树；
④ 后序遍历树 ≡ 中序遍历该树对应的二叉树。

树、森林与二叉树的转换

树转化为二叉树

1、将树的各兄弟结点连线
2、每个结点仅保留于其长子的连线，去掉该结点与其他子结点的连线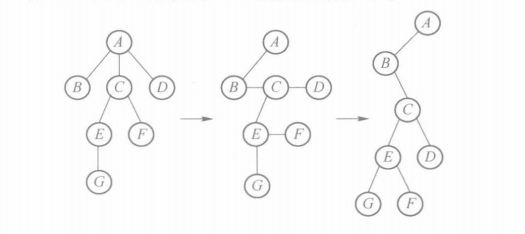

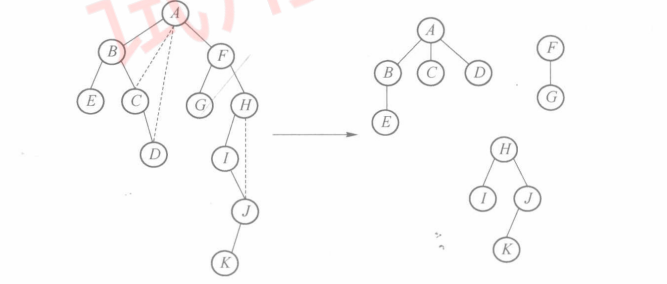
森林转化为二叉树

先把每个树转化为二叉树然后再把每个树的根结点连线作为兄弟节点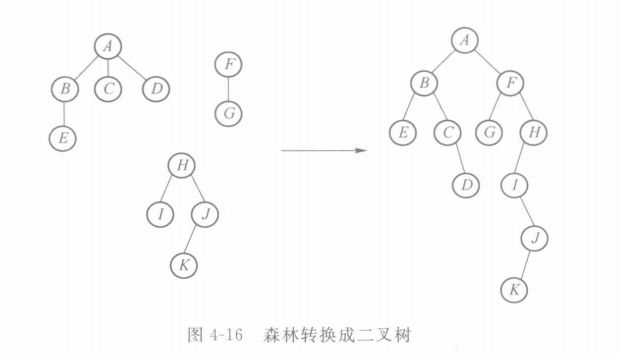

二叉树转换为树、森林

如果一个节点 x 是它双亲 y 的左孩子，那就要把 x 的右孩子、x 右孩子的右孩子这些，都直接和 y 连起来。连好之后，把所有双亲到右孩子的连线都去掉